Ad Servers play a big role in the profitability of many media companies. Many of these media companies are niche companies with narrow audiences and have fewer advertisers than, say, a mega media company like Google. For these blogs, I am specifically discussing niche media companies where the number of eligible ads is small. My example considers only 6 eligible ads. I imagine these techniques might work well for up to 20 eligible ads.

The figure to the right shows the distribution of past Placement decisions of six of our eligible ads. There are 21 possible slots for each ad and one option that excludes the ad for a total of 22 possible options for each Ad.
Simple nomenclature for Ad Placement is used: cPs where c = Ad Count of the Ad Set R and s = slot number where s=1 is top and s=Ad Count is the bottom slot. 4P3 is slot 3 in a 4 ad set.
A big assumption
I find little literature that will quantify Risk of Sales. My assumption is that Caliber of Sales = 1/Risk. Risk to the disruption of sales becomes measurable. Caliber of Sales is the measure of how impervious the business is to a disruption of sales.
Likewise the word “Goodwill” is nearly taboo to accountants. It’s definition is nebulous at best. When a company is acquired by another, the acquirer records the the intangible assets of the purchase as Goodwill. They will often buy market share (intangible asset) or new customers (another intangible asset). It is this value of continued sales that I call Goodwill.
Since most media companies have little in the way of hard assets, the value of goodwill is really most of their value.
Goodwill = Θ k Sales / Sales Risk
Goodwill = Θ k Sales Caliber(Sales)
where Θ with range {0,1} is the CEO’s (or investor’s) Aversion to Sales Risk, and k is the company’s sales to value multiple (Stock Value / Sales). Caliber of Sales is the entropy associated with the Sales Distribution.
Caliber of Sales = Caliber(Sales) = ∑ – p(i) log p(i)
where p(i) is percentage sales of customer i.
The goal of the ad server is to find the Ad Set that is expected to have the greatest Equity or sum of Profit and Goodwill.
max –> Equity = Profit + Goodwill
max –> Profit + Θ k Sales Caliber(Sales)
max –> Profit + Θ k (Profit/m) Caliber(Sales))
max –> Profit (1+ Θ k Caliber(Sales)/m)
⇑ 2 factors to optimize ⇑
The extreme cases:
A uniform Sales distribution will have the maximum possible Caliber and lowest Risk. Uniform means each customer produces same amount of sales. In our example uniform sales distribution means each ad (customer) would produce 1/6th or 16.6% of sales. 6 customers with a uniform distribution is 2.58 bits of Caliber. This ideal ad set mix represents the maximum possible Caliber of 2.58 bits (maximum entropy) and minimum possible Risk = 1 / 2.58 bits = 0.38/bit .
A Sales distribution to a single customer is the highest possible Sales Risk and has zero Caliber. If Ad Count = 1 then there is no Goodwill or Caliber only Profit. It is important to note that Caliber and Goodwill are a measure of an ensemble of ads. Goodwill or Caliber are ‘macro’ variables of the ad server. They are measures of an ad set. No individual ad has a property called Caliber or Goodwill, only Ad Sets (or resulting total Sales distribution) do.
Example Optimization of Equity of an Ad Set
Our example has a simple Ad Serving Policy:
- No ad or Brand may be shown more than once
- No two ads can be placed in the same position
- 1 <= Ad Count <= 6
Given this Policy how do we find the optimum Ad Set that will produce the most Profit + Goodwill? We need four additional variables which are:
- Evidence e [Context1 and Context2] which help predict performance for Ads C, D and F
- Price per ad Click (as the model above) or Price per Approval, or in general, Price per Action. (I used 14 eligible ads with a wide range of response and pricing)
- From our prediction model p(outcome | Placement, e) for each Ad. (used old ad data)
- CEO(investor’s) Aversion to Risk Θ. (assume that Θ = 0.9)
- Current Sales Distribution
- The Value to Sales ratio used in this simulation is 2.0 and is Stock Value / Annual Sales.
- The margin m is 0.30.
Algorithm to find Max Equity
- For each possible AdCount DO:
- Max Profit: Find the Ad Set with greatest Profit
- for n = 1 to 6
- from all eligible ad placements, select the ad placement with greatest expected Profit
- Calculate Profit and Equity of this Ad Set
- for n = 1 to 6
- Max Caliber: Do Until change in Equity is not positive:
- For each ad selected above, calculate the Gain in Caliber per lost revenue if this ad is swapped with another ad.
- Select the ad swap that produces maximum Caliber gained per lost Profit (max entropy).
- If change in Equity is positive, make the swap
- Max Profit: Find the Ad Set with greatest Profit
- Select Ad Set with greatest Equity
Algorithm 2 to find Max Equity
This algorithm uses a strategy called Freedom of Choice to find the first Ad Set. If we have X eligible ads with 6 possible slots, then initial number of Choices is n = 6X. Freedom of Choice = log n. Of all the choices (6X) that we can make which choice produces the maximum Profit per depleted Freedom of Choice?
Lost Freedom of Choice = log (n before decision) – log(n after decision)
Freedom of Choice algorithm is helpful if customers have multiple ads but the Server Policy allows a single ad per customer (Brand) to be shown.
- For each possible AdCount DO:
- Max Profit per lost Freedom of Choice: Find the Ad Set with greatest Profit
- for n = 1 to 6
- from all eligible ad placements, select the ad placement with greatest expected Profit per lost Freedom of Choice
- Calculate Profit and Equity of this Ad Set
- for n = 1 to 6
- Max Caliber: Do Until change in Equity is not positive:
- For each ad selected above, calculate the Gain in Caliber per lost revenue if this ad is swapped with another ad.
- Select the ad swap that produces maximum Caliber per lost Profit.
- If change in Equity is positive, make the swap
- Max Profit per lost Freedom of Choice: Find the Ad Set with greatest Profit
- Select Ad Set with greatest Equity
Results of Simulation
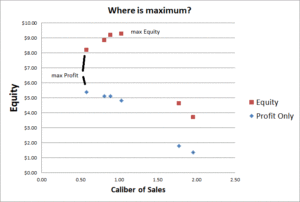
Step 1 of the algorithm is done is 6 steps to find maximum Profit of $5.36. Goodill was low because this ad set sold most to big customers with large sales distribution. Goodwill of the max Rev Ad Set is $2.82 for a total Equity of $8.18.
Step 2 of the algorithm was done in 3 loops (jiggles). The final optimum Ad Set produced $4.80 in Profit and $4.46 in Goodwill. Maximum Equity = $9.26
| Sales | Caliber | Goodwill | Profit | Equity | |
| $17.88 | 0.58 | $2.82 | $5.36 | $8.18 | Max Sales |
| $16.99 | 0.81 | $3.72 | $5.10 | $8.81 | Using Caliber of Choices strategy |
| $16.97 | 0.89 | $4.09 | $5.09 | $9.18 | C of C with a Jiggle |
| $15.99 | 1.03 | $4.46 | $4.80 | $9.26 | C of C with 2 Jiggles |
| $5.91 | 1.78 | $2.84 | $1.77 | $4.61 | High Caliber |
| $4.46 | 1.96 | $2.36 | $1.34 | $3.69 | Near Maximum Caliber |
Conclusions
 CEO’s and investors alike want high profit and low risk business. They want a high Caliber business that can withstand disruptions to sales to customers. Yet there is little agreed upon method to measure this risk or the value produced when reducing risk. Caliber of Sales is this missing variable.
CEO’s and investors alike want high profit and low risk business. They want a high Caliber business that can withstand disruptions to sales to customers. Yet there is little agreed upon method to measure this risk or the value produced when reducing risk. Caliber of Sales is this missing variable.
I have seen ad servers show a single ad, when other ads are eligible because this advertiser bids so high. Yet the Caliber of Sales of a single customer is zero. A business with a single customer has the greatest risk from sales disruption. Is a business with a single customer a real business?
Ad Servers can help solve the problem of customer concentration using Caliber.

