Fundamental Equation of Business Potentials

Since I was a student of mechanics and physics a better understanding has emerged. Hamiltonian and Lagrangian math has revealed a single method from which the “Laws of Nature’ can be derived. The method is to choose a coordinate system, write the Hamiltonian, assume some initial conditions and then solve the “Saddle” equations. This calculus has been used to derive Newton’s Laws of Motion. It solves 3 body celestial problems, solves any mechanical device’s future motion, it explains solutions in quantum mechanics, all of Maxwell’s equations, Kirchhoff’s principles, Fourier’s heat transfer. I have not seen this math applied to business.

The Laws of Motion of business would predict future states of the business. This math could be very helpful to managers wishing to obtain better performance from the company. Since business is the practice of goal seeking they really want to control the business so that some performance is maximum. Hamiltonian math can find the optimal control u(x,t) that will produce maximum performance. It also can produce the trajectory of variables in business. These are the laws of motion.

To begin we need to pick a coordinate system that will describe the business. Business already uses a host of metrics to account for its states. The English language surrounding business also seems a natural fit for the problem. The main coordinate for business is cash. Let cash be free Energy. Free cash flow is a company’s production of Free Energy.

Energy, Entropy and Temperature

The physical world is well described using models that involve Temperature, Entropy and physical coordinates (Voltage, pressure, volume, conductance). A Carnot Heat Engine is a simple model of how to extract Work from a Temperature potential. Here entropic forces generate work from a machine between two temperatures. Electric circuits dissipate energy when entropic forces push current through an conductance. Potential energy causes current to flow through the conductance which dissipates energy. This figure models a business using the same language (coordinates).

Imagine businesses are bubbles that conduct business by touching after agreement on terms: N, t, and price. This price is phi. Rho is the conductance that allows a given flow rate. The product of N and phi is cash flow or change in energy. Likewise I think a model business will include Entropy along with business metrics (Sales, Costs, Budget, Market Cap, Goodwill, Risk) and can be very helpful for making decisions.

Fundamental Equation of Business Potentials

For a time period τ the change in value of a business dU is the change in internal energy less the cost of work plus the change in sales plus changes forced by external variables.

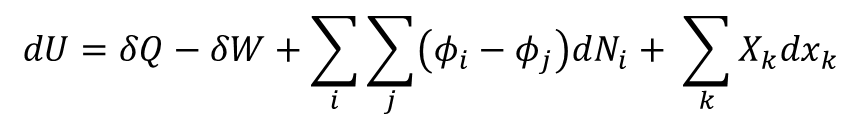
U is business value
Q is internal energy of business including cash
W are costs of operations
ϕ_i  is price paid by customer i
ϕ_j  is price paid to supplier j
N_i, is number of units sold to each customer i. It is a vector with length i.

Sales Sustainability and Sales Caliber

Investors and business managers insist on sustainability. They hate risks to ongoing sales. Business managers reduce sales risk by selling to many customers and then distributing sales to its customers. I propose using Sales Caliber as a measure of a business’s sales sustainability. Sales Caliber is the Shannon Entropy of the Sales Distribution (named “Caliber” by E.T. Jaynes).

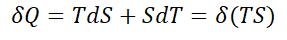
Three example sales distributions are shown below. Business/Marketplace C has fewest customers and 95% of sales are to one customer (intense sales concentration risk):

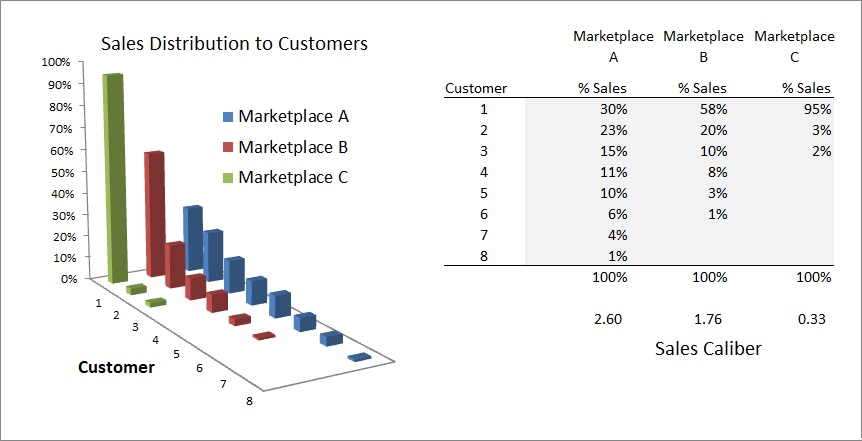
Caliber of Sales, S, is a direct measure of the certainty of future sales. Likewise, 1/S, is the Risk of future Sales. If T is profit margin, then TSN represents business’s potential energy from future sales. Caliber is a continuous measure of sustainability making it a very helpful metric for business managers. Said another way:  Goodwill = T x Sales Caliber x N

The change in internal energy is the sum of the margin T times change in Caliber S plus the Caliber S times the change in margin T.

Business Value as Total Energy

If we take the Fundamental Equation, substitute the above, and integrate over time tau or over N, we get:

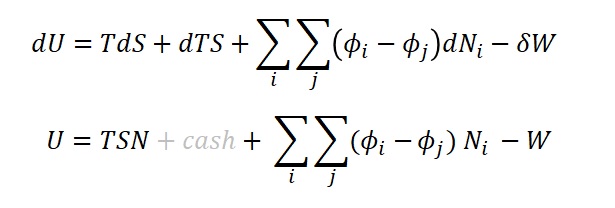
These equations simply sum the energy provided the business in the form of potentials. These are the energy equations of business with external forces excluded.

Business Performance Measures

Most of standard business metrics can be found by knowing the value of each variable in the energy equations. Here is a selection of business performance metrics.

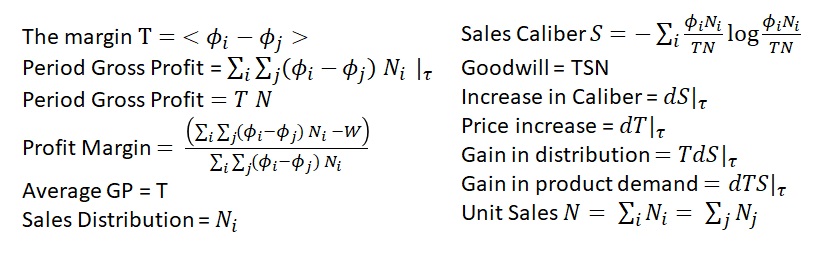
Optimizing Business Performance

Every business is seeking a goal and I think success comes mostly to business with well considered goals. Here are the variables of the business:

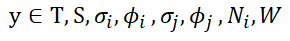
Not all of these variables are accessible to the business. Example, in an auction setting the customer sets the price phi i. Typically some performance J is to be maximized over the next month, quarter, or next several years (over some time period τ).

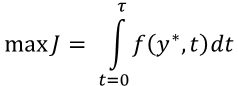
Imagine that the goal of a young business is to produce maximum TdS each quarter whatever other y may become. Then the performance function is:

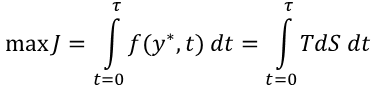
f(y,t)=TdS. The business does this by changing the vectors σi and Ni  . This maximum can be computed very quickly and will have an optimal Ni  ^* distribution of product given the goal.

This maximum occurs when the partial derivative of f with respect to Ni is 0. Ni is our control u below:

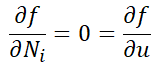
This solution was very easy with no constraints. Real business goals most often have constraints of allowable business states. In the above J we might add a constraint that gross profit margin T must be > 13%. But still the last expression is true del f /del u = 0

Another goal might be to maximize gross profit. To accomplish this goal, the entropy of the business is depleted (exemplifying that it is potential). To maximize gross Profit by adjusting N_i, we simply deliver all N units to customer with greatest price ϕ_i. The entropy of such a distribution is 0, produces maximum temperature T and is least sustainable state of the business with S=0. This is a bad goal without constraints.

The Hamiltonian

Now that we have a general form for performance J and the energy equations of business, we can write the Hamiltonian:

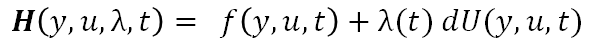
with performance function f:

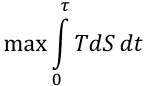
The Hamiltonian is:

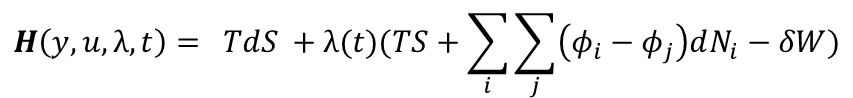
If a pair (u*(t), y*(t)) is optimal then there exists a continuously differentiable function λ(t) such that:

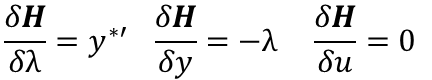
Business Laws of Motion

These partial differential equations predict the final state of the business when management applies changes to a control. In our example the control u is N_i, and the prediction is the optimum Temperature and change of Entropy (T*,dS*) given the performance goal of the business. They are a way to calculate values of all other variables of the business model at time:

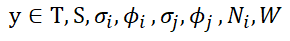
The function λ(t) is a Lagrangian transformation. We begin finding the optimal control using the last equation and then calculate each other variable in y using the first two equations.

To be clear, a business has a limited number of variables y that it can control and which describe it’s periodic performance. Any ‘law of motion’ will include the variables in the energy equation of the business. The laws of motion y(t) and y’(t) can be calculated by solving the Hamiltonian differential equations on a computer with Python. Those variables in y not in the control can be forecast or predicted.

Lastly

The equations of motion of a business predict the state of business after a time τ. By applying a performance function and the energy function (aka business potentials) of the business to form the Hamiltonian, we can then estimate the state of all other variables in the collection y.

TSN + cash is the potential energy of a business. Free cash flow is kinetic energy.

It is clear that a company should optimize it’s distribution of products to produce Entropy. “The goal of business is to produce entropy”. Who said that? Seems that in business Entropy can decline if managers choose to begin selling product to fewer customers or if customers choose to stop buying.

A more modern accounting of business would include formal reporting of TdS and dTS, and TSN. Investors are more interested in future potential of the business. This is best estimated with the internal energy TSN which is the business asset Goodwill which encompasses: (price, distribution, volume).

References

1. Wayne, James J., 2013. “Fundamental Equation of Economics,” MPRA Paper 50695, University Library of Munich, Germany.
2. Kirk, Donald,J., 1967, “Optimal Control Theory”, Prentice Hall
3. Hamill, Patrick, 2014, “Lagrangians and Hamiltonians: A Student Guide to”, Cambridge University Press
4. Jaynes, E.T., “The Minimum Entropy Production Principle“,
5. WikiPedia, “Thermodynamic Potential“,