Entropy and Temperature for a Book of Orders

Entropy and a Book of Orders

In thermodynamics, Heat, Temperature, Pressure, Work and Entropy are the main ensemble of variables that describe how mechanical/cyclical engines operate. The second law of thermodynamics was a big deal when it was discovered. The models of the cycle of these engines sparked the industrial revolution. Example the Carnot Heat Engine. Chemistry and chemical engineering fields also enjoyed a boon of discoveries and applications and products. All these are bound and constrained by this notion of Entropy.

Around the same time, late 1800s, Willard Gibbs ‘discovered’ the same Entropy in statistical models of the world. This statistical Entropy worked the same way as physical entropy. Later in the 1950s Claude Shannon ‘discovered’ Entropy at Bell Labs as it relates to communications (conveying information). This entropy also obeyed the second law. Again it was a boon to understanding and building communication systems of all kinds.

I think that in the business world probabilistic models can be applied to model cyclic processes like click advertising and lead generation (supply and demand problems). Gibbs Entropy, I believe, can be used to understand the limits, constraints and optimizations of the process. I believe that these business cycles will indeed obey the second laws of thermodynamics. The ensemble of Variables in advertising: Profit, Profit Margin and Entropy are analogous to Work, Temperature and Entropy in engines. Humans seem to understand entropy well. We are constantly weighing options while we all seek our own utility. Acting to get more energy than we expend. We watch around us as once ordered things decay, rust, stop working, crumble. Famously, Claude Shannon at AT&T made the the connection between Entropy, bandwidth and information content.

I have abducted his Theorem (actually others are calling it Gibbs-Shannon Entropy) and eagerly explore this same entropy as an oracle for decision making for optimal consumption, in this case, an optimum ad serving strategy.

I think we can calculate the value of a Book of CPC advertisers using Entropy. The Book is the full collection of all your CPC client Orders. “Book” for short. Temperature of the Book T is the difference between Sales (RPV) and Cost (CPC). Total Book value = Sum of (Entropy x T)

This concept applies to certain difficult marketing businesses.

• An example system is Ad Serving, the business of choosing the ads to place on web pages given a Book of Ad Orders X, an uncertain supply of page views, ad placement and ad responses Y, and an uncertain user demographic and context variables Z, where Z∈Y.
• Likewise applicable is the internet Lead business where a Book of Orders for Leads X is sold into an uncertain supply of Leads and lead disposition variables Y that also have uncertain lead demographic and source (context) variables Z, where Z∈Y.

In these businesses the Book of Orders (Book for short) is a company asset. It fairly can be put on the company’s Balance Sheet as the predicted sum of profit from the full depletion of the Book. It presents the ability to generate revenue in the future. The marketer’s goal is to deplete this Asset and produce the most profit for the company from this asset.

Entropy H(x) associated with a single Order x.

I propose that the value of this asset is proportional to the Entropy associated with the Book of Orders. The value of the Book is product of the associated Entropy H(X) and the expected gross profit of a sale (Sales T_X – Cost of Sales W_X – Cost of Goods T_Y).

Value = ∑_z H(X) ( ΔT – W_X)  analogous to Total Energy = Σ H(x) Δ T

And here are some framework notations for a Book of Orders:

Let us define the common parameters of Orders and of supply.

• The probability of a match for Order x_i = p( x_i | z) where z are the order selection variables in set of Z where Z∈Y.
• We know that the probability of a match is the probability that supply Y is in the same demographics, so p( x_i | z) = p( Y|z). Probability of a match is based on supply.
• T_xi is the price of Order x_i. Let n be the quantity of the Order or the maximum acceptable quantity in a time period. And T_Y(z) is the expected Cost of an instance of the supply y_i(z). Profit for a filled order = Revenue – Cost of Revenue – COGS= T_xi – T_Y(z) – W_X
• Y contains a set of response variables and Do variables that denote a sales funnel which form a Markov chain ( y1 –> y2 –> y3 …).

Entropy associated with Order x = H(x) = n ∑_x∈Y  – p( Y|x ) log_b p( Y|x ). Note that if an order falls outside of Y (x∉Y), the Entropy associated with x is zero and the order will have no value. Maximum entropy occurs when p(Y|x) = 1/2. Using log base 2 gives units of bits for the entropy.  However, Jing Chen, in his paper “The Entropy Theory of Value” says that b is the number of producers of Y. hmm.

Equity of an Order

Equity is Energy. Relative Temperature is ΔT = T_X – T_Y or the difference in sales and cost (gross profit).  The Balance sheet Equity E that is generated by an new Order  is

E = ∑_z H(x_i) ( T_xi – T_Y(z) – W_X)      or  E = ∑_z H Δ T    or  Equity = Entropy x Change in Temperature

Likewise Equity is produced if Entropy increases while Temperature is held steady. E = T Δ H

The per Unit value of a drawn lead or page-view is V(Y|x) = – log₂ p( Y|x ) is the log likelihood of a match and is = the number of true/false questions needed, on average, to guess if a match for order x has occurred.

Equity of more than one order – a Book

Entropy of two orders and Mutual Information of the Orders

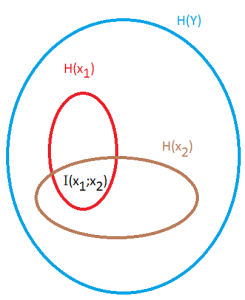
Entropy of two Orders x₁ and x₂  = H(X) = H(x₁ ,x₂ )

In general, H(x₁ ,x₂ ) ≤ H(x₁ ) + H(x₂ ). This means the book entropy can be less than the sum of entropy for each order. Equality occurs when x1 and x2 are independent.  When two Orders overlap they have mutual information I.

H(x₁ ,x₂ ) = H(x₁ ) + H(x₂ ) – I(x₁ ;x₂ ) where I(x₁ ;x₂ ) is the Mutual Information of the two orders.

By Chain Rule, the Entropy of three Orders = H(X) = H(x₁ ,x₂ ,x₃) = H(x₁ ) + H(x₂ | x₁) + H(x₃ | x₂ , x₁)

The chain rule offes an algorithmic approach to calculating the Entropy of a Book. The series has k calculations. Book Entropy of k Orders = H(x₁,x₁,x₁,…, x_k)

Total Value of a Book of Orders = ∑_x  H(X(x)) (ΔT(x))